Grundlegende Stromkreise
Diese kleine Übersicht soll als kleine Stütze zum Thema Elektrizitätslehre als Begriffserläuterung dienen. Mögliche Fehler sind vorbehalten, es wird keine Garantie auf Richtigkeit gegeben. Diese Übersicht behandelt lediglich Gleichstrom Stromkreise, da Wechselstrom Stromkreise komplinzierter sind und von mir in Basteleien generell nicht verwendet werden.
Achtung! Stromkreise sind mit äußerster Vorsichtig zu behandeln! Experimente sollten ausschließlich mit maximal 24Volt Gleichspannung durchgeführt werden. Ein Laie hat nichts an Hausstromkreisen zu suchen.
Grundlegendes
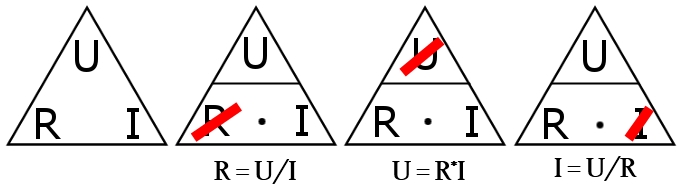
Es gibt drei Grundlegende Dinge in Stromkreisen: der elektrische Widerstand, die Spannung und der Strom (bzw die Stromstärke). Folgend die Formelzeichen, deren Einheiten und der Rechenweg “ / “ symbolisiert entweder einen Bruchstrich oder ein „geteilt durch“, “ * “ symbolisiert ein „mal“.
Widerstand • Formelzeichen: R • Einheit: Ohm ( Ω ) • Rechenweg: R=U/I Spannung • Formelzeichen: U • Einheit: Volt ( V ) • Rechenweg: U=R*I Stromstärke • Formelzeichen: I • Einheit: Ampere ( A ) • Rechenweg: I=U/R Kleiner Tipp zum Merken der Formeln: Das URI-Dreieck
Stromkreislauf
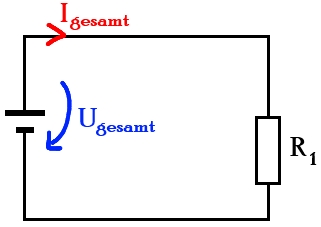
Jedes Gerät basiert auf sog. Schaltplänen. Diese stellen das Grundgerüst dar, bevor irgendetwas gebaut wird, wird ein solcher Schaltplan in der Regel aufgestellt. Dies hilft zu sehen, wo es ggf. noch Probleme gibt und voralledem bei Problemlösungen. Ein Stromkreislauf muss geschlossen sein, damit ein Strom fließen kann. Ist dies nicht der Fall, fehlen entweder z.B. Verbinden (Kabel), ein Schalter ist nicht aktiviert oder es besteht ein Wackelkontakt. Folgend ein sehr einfaches Beispiel eines Schaltplanes. In ihm ist die Stromquelle U, die Stromstärke I und ein Widerstand R (1) eingezeichnet. Dieses Beispiel dient zur Veranschaulichung und wird später immer wieder aufgegriffen.
Mit diesem Wissen, können wir uns nun näher mit Reihen- und Parallelschaltungen beschäftigen.
Alles zum Thema Elektrizitätslehre: Reihen- sowie Parallelschaltung (2/2)